今天灿爷模拟赛
灿爷预计平均分60
结果比他预计的高了40+...
打满三题暴力110分
实力RANK11 233
好吧其实只是因为四川大爷走了
一试不慎爆蛋的也走了 人变少了
今天不知道在干啥……做的题和明天并起来好了
不用点开没东西了
UPD Apr.1st 今天做了十多道April Fool Contest做傻了……明后天再来更
计算几何(%mjy)
考虑一个凸四边形,随意选其中三个点,
当那三个点构成的角和其对角加起来超过180°时,
这三个点构成的外接圆能覆盖4个点,
否则只能覆盖3个点
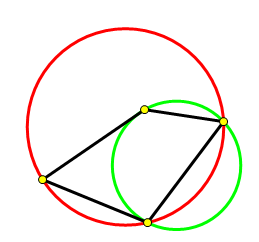
再考虑一个凹四边形,只有选外围3个点时,
才能覆盖全都4个点,否则只能覆盖3个

然后我们枚举凹四边形中间那个点,
算出以这个点为中心的凹四边形有几个
这个可以通过以这个点为一个顶点的四边形总数减去凸四边形的数量
凸四边形的数量可以通过两个指针维护,
只要两边差不超过180°就可以了
然后加起来,而凸四边形的数量就是所有四边形的数量减掉凹四边形的数量
就可以算了
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>
#include<ctime>
#include<cstdlib>
#include<string>
#include<queue>
#include<cmath>
#include<set>
#include<map>
#include<bitset>
#include<vector>
#define Rep(x,a,b) for (int x=a;x<=b;x++)
#define Drp(x,a,b) for (int x=a;x>=b;x--)
#define Cross(x,a) for (int x=head[a];~x;x=next[x])
#define ll long long
#define INF (1<<29)
#define mk(a,b) make_pair(a,b)
#define fr first
#define sc second
using namespace std;
inline ll IN(){
ll x=0;int ch=getchar(),f=1;
while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar();
if (ch=='-'){f=-1;ch=getchar();}
while (isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
inline void OUT(ll x){
if (x<0) putchar('-'),x=-x;
if (x>=10) OUT(x/10),putchar(x%10+'0');
else putchar(x+'0');
}
const int N=1505;
const double pi=acos(-1.0);
struct Poi{
int x,y;
double Ag;
bool operator <(const Poi&w)const{return Ag<w.Ag;}
}a[N],b[N];
ll cross(Poi A,Poi B,Poi C){
return 1ll*(B.x-A.x)*(C.y-A.y)-1ll*(C.x-A.x)*(B.y-A.y);
}
ll n,H;
int main(){
n=IN();
Rep(i,1,n) a[i].x=IN(),a[i].y=IN();
ll Ans=0;
Rep(i,1,n){
b[0]=a[i];
Rep(j,1,i-1) b[j]=a[j];
Rep(j,i+1,n) b[j-1]=a[j];
Rep(j,1,n-1) b[j].Ag=atan2(b[j].y-b[0].y,b[j].x-b[0].x);
sort(b+1,b+n);
Ans+=(n-1)*(n-2)*(n-3)/6;
int T=2,L=0;
Rep(j,1,n-1){
while (cross(b[0],b[j],b[T])>=0){
T=T%(n-1)+1,L++;
if (T==j) break;
}
Ans-=L*(L-1)/2;L--;
}
}
ll NoR=n*(n-1)*(n-2)*(n-3)/24,NoT=n*(n-1)*(n-2)/6;
ll Four=NoR*2-Ans;
printf("%.6lf\n",(4.0*Four+3.0*(NoT-Four))/NoT);
}
并查集
画个图找一下规律,
会发现确定了第一行和第一列以后,
整张图都是确定的,并且
$a_{i,j}\ xor\ a_{i,1}\ xor\ a_{1,j}\ xor\ a_{1,1}=[i是偶数且j是偶数]$
然后就可以用带权并查集啦~
首先读入限制时如果 $i,j$ 都是偶数就把颜色反一下
先假设$a_{1,1}=0$,然后
如果$a_{i,j}=0$,那么说明$a_{i,1}$与$a_{1,j}$相同,否则颜色不同
这样跑一边并查集
如果有矛盾的话答案就是0
否则答案就是$2^{连通块个数-1}$(要去掉 $1,1$ 所在的连通块)
然后假设$a_{1,1}=1$,把限制全都反一下
再跑一遍就可以了
注意如果限制里有规定 $1,1$ 的颜色的话要特判一下
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>
#include<ctime>
#include<cstdlib>
#include<string>
#include<queue>
#include<cmath>
#include<set>
#include<map>
#include<bitset>
#include<vector>
#define Rep(x,a,b) for (int x=a;x<=b;x++)
#define Drp(x,a,b) for (int x=a;x>=b;x--)
#define Cross(x,a) for (int x=head[a];~x;x=next[x])
#define ll long long
#define INF (1<<29)
#define mk(a,b) make_pair(a,b)
#define fr first
#define sc second
#define MOD 1000000000
using namespace std;
inline ll IN(){
ll x=0;int ch=getchar(),f=1;
while (!isdigit(ch)&&(ch!='-')&&(ch!=EOF)) ch=getchar();
if (ch=='-'){f=-1;ch=getchar();}
while (isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
inline void OUT(ll x){
if (x<0) putchar('-'),x=-x;
if (x>=10) OUT(x/10),putchar(x%10+'0');
else putchar(x+'0');
}
const int K=1000005,N=2000005;
struct Paint{
int x,y,c;
}a[K];
int Fa[N],De[N],Va[N];
int getfa(int x){
if (Fa[x]==x) return x;
int F=Fa[x],ZF=getfa(F);
Va[x]=Va[x]^Va[F];
return Fa[x]=ZF;
}
int n,m,k,Tm,Vs[N];
int Pow(int Bs,int Zs){
int ret=1;
for (;Zs;Bs=1ll*Bs*Bs%MOD,Zs/=2) if (Zs&1) ret=1ll*ret*Bs%MOD;
return ret;
}
ll Ans;
void GetAns(){
Rep(i,1,n+m-1) Fa[i]=i,Va[i]=0,De[i]=0;
bool Cd=1;
int Ks=n+m-1;
Rep(i,1,k){
int x=a[i].x,y=a[i].y==1?1:a[i].y+n-1,col=a[i].c;
int Fx=getfa(x),Fy=getfa(y);
if (Fx==Fy){
if (Va[x]^Va[y]^col) return;
}
else{
if (De[Fx]==De[Fy]) De[Fx]++;
else if (De[Fx]<De[Fy]) swap(Fx,Fy);
Va[Fy]=Va[x]^Va[y]^col;
Fa[Fy]=Fx;
Ks--;
}
}
if (Cd) (Ans+=Pow(2,Ks-1))%=MOD;
}
int main(){
n=IN(),m=IN(),k=IN();
bool _0=1,_1=1;
Rep(i,1,k){
a[i].x=IN(),a[i].y=IN(),a[i].c=IN();
if (a[i].x==1&&a[i].y==1){
if (a[i].c==1) _0=0;else _1=0;
i--,k--;
}
else if (a[i].x%2==0&&a[i].y%2==0) a[i].c^=1;
}
if (_0) GetAns();
if (_1){
Rep(i,1,k) a[i].c^=1;
GetAns();
}
OUT(Ans);
}
Aug 25, 2022 02:34:18 PM
Meghalaya Board Model Paper 2023 Pdf Download for the State School Education Board (MBOSE) Sample Model Question Paper for Class 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 Grade Bengali Medium, Hindi Medium, English Medium and other Medium Theory, Objective (MCQ) and Bit Questions. MBOSE Question Paper New Exam Scheme or Question Pattern for Sammittive Assignment Exams (SA1 & SA2): Very Long Answer (VLA), Long Answer (LA), Small Answer (SA), Very Small Answer (VSA), Single Answer, Multiple Choice and etc.
Apr 16, 2023 06:43:14 PM
TeachersBadi is information about education, students and teachers.‘TeachersBadi‘, the name itself discloses the nature of the site. The site is being launched and run by a dedicated Team for teachers, students and educators. We love to share mainly educational information teachersbadi.in and employees, teacher’s related content in the education world.